मैक्सवेल के विद्युत चुंबकत्व के नियमों के चार समीकरणों में से एक गॉस का नियम है। यह शुरू में कार्ल फ्रेडरिक गॉसद्वारा वर्ष 1835 में तैयार किया गया था। गॉस के नियम में कहा गया है कि किसी दिए गए सतह के माध्यम से दिए गए विद्युत क्षेत्र का शुद्ध प्रवाह, संलग्न आवेश से विभाजित एक स्थिरांक के बराबर होना चाहिए।
गॉस का नियम
गॉस के नियम के अनुसार, किसी बंद पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स उसके अंदर उपस्थित कुल विद्युत आवेश का 1/ε0गुना होता है।
जहां ε0निर्वात अथवा वायु की विद्युतशीलता है ।
उदाहरण के लिए,
एक बिंदु आवेश q को किनारे 'a' के घन के अंदर रखा गया है। अब गॉस नियम के अनुसार, घन के प्रत्येक फलक से गुजरने वाला फ्लक्स q/6ε0है।
विद्युत क्षेत्र बिजली के बारे में जानने की मूल अवधारणा है। आमतौर पर, सतह के विद्युत क्षेत्र की गणना कूलम्ब के नियम को लागू करके की जाती है, लेकिन एक बंद सतह में विद्युत क्षेत्र के वितरण की गणना करने के लिए, हमें गॉस कानून की अवधारणा को समझने की आवश्यकता है। यह एक बंद में संलग्न विद्युत आवेश या संलग्न बंद सतह में मौजूद विद्युत आवेश की व्याख्या करता है।
गॉस के नियम का सूत्र
एक बंद सतह में संलग्न कुल आवेश सतह से घिरे कुल फ्लक्स के समानुपाती होता है। इसलिए, यदि कुल फ्लक्स है और ϵ0 विद्युत स्थिरांक है, तो सतह से घिरा कुल विद्युत आवेश Q है;
गॉस नियम सूत्र द्वारा व्यक्त किया जाता है,
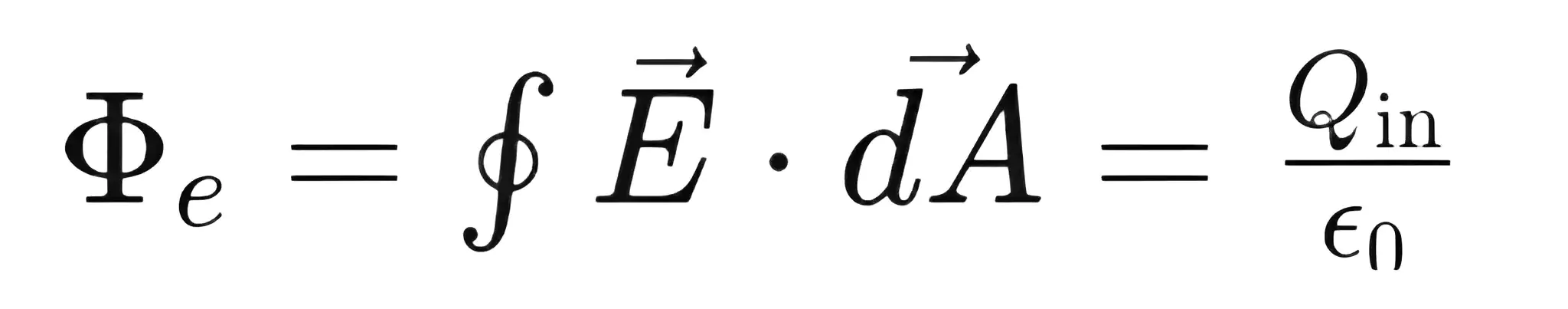
गॉस का प्रमेय
एक बंद सतह के माध्यम से शुद्ध प्रवाह सीधे बंद सतह से घिरे मात्रा में शुद्ध आवेश के समानुपाती होता है।
ϕ=Q/ε0
सरल शब्दों में, गॉस प्रमेय विद्युत क्षेत्र रेखाओं (फ्लक्स) के 'प्रवाह' को संलग्न सतह के भीतर आवेशों से संबंधित करता है। यदि किसी पृष्ठ से कोई आवेश संलग्न नहीं है, तो शुद्ध विद्युत फ्लक्स शून्य रहता है।
गॉस के नियम के अनुप्रयोग
- अनंत विस्तार की रेखीय आवेश के कारण विद्युत क्षेत्र की तीव्रता निकालने में।
- समरूप अनंत विस्तार की आवेशित कुचालक चादर के कारण विद्युत क्षेत्र निकालने में।
- अनंत विस्तार की समरूप आवेशित चालक प्लेट के कारण विद्युत क्षेत्र की तीव्रता निकालने में।